Jano zadal nasledujúci príklad:

Pre tých, čo neovládajú azbuku a ruštinu prekladám. V štvoruholníku ABCD
je AB = BC = CD a uhly pri vrcholoch A a B sú 70 a 100 stupňov.
Aké sú uhly pri vrcholoch C a D?
Skonštruovať štvoruholník je jednoduché a priamočiare a dosť rýchlo si
uvedomíme, že trojuholník BCD je asi rovnostranný. Ja rád rysujem
klasicky na papier, aj rád používam Geogebru. V nej si to overíme
úplne presne.
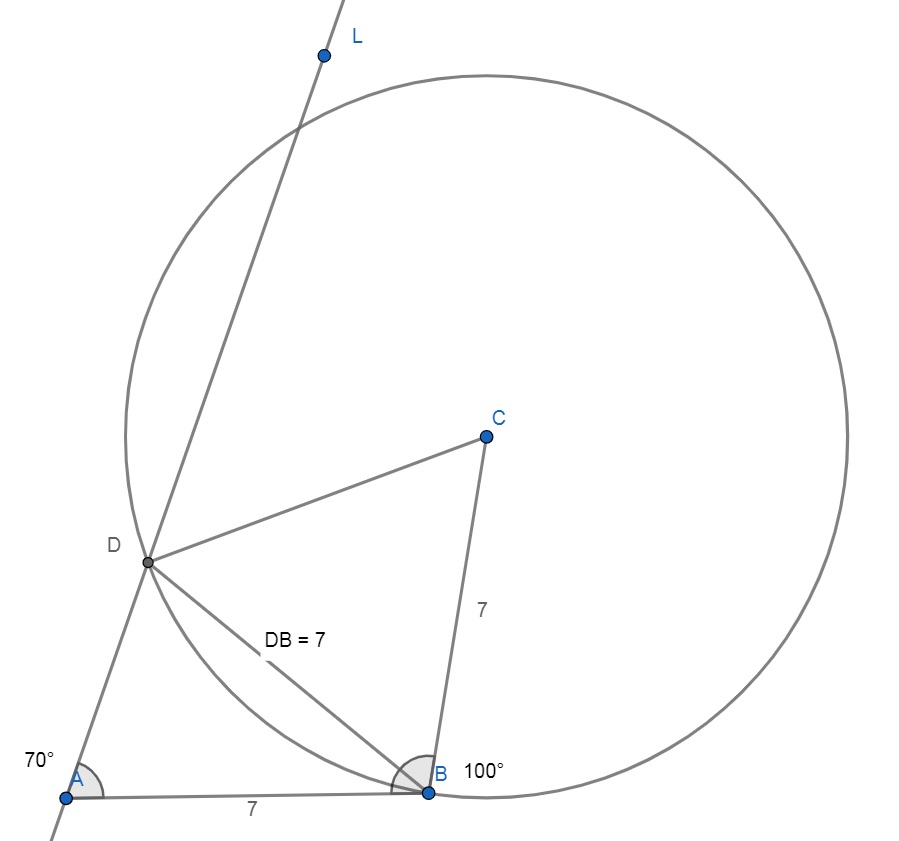
To samozrejme nie je riešením úlohy, ale veľmi ľahko ukážeme,
že keď je trojuholnik BCD rovnostranný a zároveň teda
keď trojuholnik ABD je rovnoramenný, že platí
\(\angle{A} = 120° - { \angle{B} \over 2 }\), čo teda presne zodpovedá
zadaniu našej úlohy. Že potom \(\angle{C} = 60° \) a \(\angle{D} = 130° \),
snáď nemusím ani písať.
Čo však musím napísať je toto: Úloha má samozrejme aj druhé riešenie,
pretože priamka AD pretína kružnicu so stredom v bode C a
polomerom BC v dvoch bodoch. To je, tak povediac, v pohode
a ďalej sa tomuto druhému riešeniu nebudem vo svojich úvahách
venovať.
Čo ale pokladám za nutné explicitne zdôrazniť je to,
že si treba dobre uvedomiť, že toto riešenie - nájdené akoby skusmo -
je riešením jedinečným. Že neexistuje nijaká iná vzdialenosť BD,
pri ktorej by bolo splnené zadanie úlohy.
Nie je to žiadna zložitá a veru ani zaujímavá úvaha,
ale z matematického hľadiska je nevyhnutná.
Zo zadania a konštrukcie vyplýva, že bod D je priesečníkom
jednoznačne určenej priamky a kružnice.
My sme síce len akýmsi spätným dôkazom dokázali, že keď
BD = AB = atď., že dospejeme k veľkostiam uhlov zo zadania,
ale to nič nemení na skutočnosti, že bod D v tejto
konkrétnej vzdialenosti od bodu B je jediným možným "vyhovujúcim"
bodom. (Ak teda ignorujeme spomínané druhé riešenie.)
Nuž ale darmo som si toto hovoril, stále som sníval
o nejakom analyticko-geometrickom riešení, z ktorého
by mi na konci nádherne vyšlo jedno jediné krásne riešenie.
Nič také sa mi dosiahnuť nepodarilo, ale absolvoval som
analyticko-geometrické cvičenie, ktorého priebeh vám tu
možno budem prezentovať, ak ma to neprestane baviť.
Takže zadaní podobných originálnemu zneniu nášho príkladu by sme mohli
vygenerovať hocikoľko, treba len dodržať už raz spomenutú podmienku
\(\angle{A} = 120° - { \angle{B} \over 2 }\). Skúsil som, či
pôjde dospieť k tejto formulke aj pomocou analytickej geometrie.
Jediné, čo môžem na úvod povedať, je to, že sa mi to teda podarilo
urobiť, ale bolo to "krvavenie", ktoré ilustruje, že na riešenie tohto typu
úloh nie je vhodné používať analytickú geometriu.
Zaviedol som súradnicový systém nasledujúcim spôsobom a veľkosť
zhodných strán štvoruholníka som položil rovnú 1.
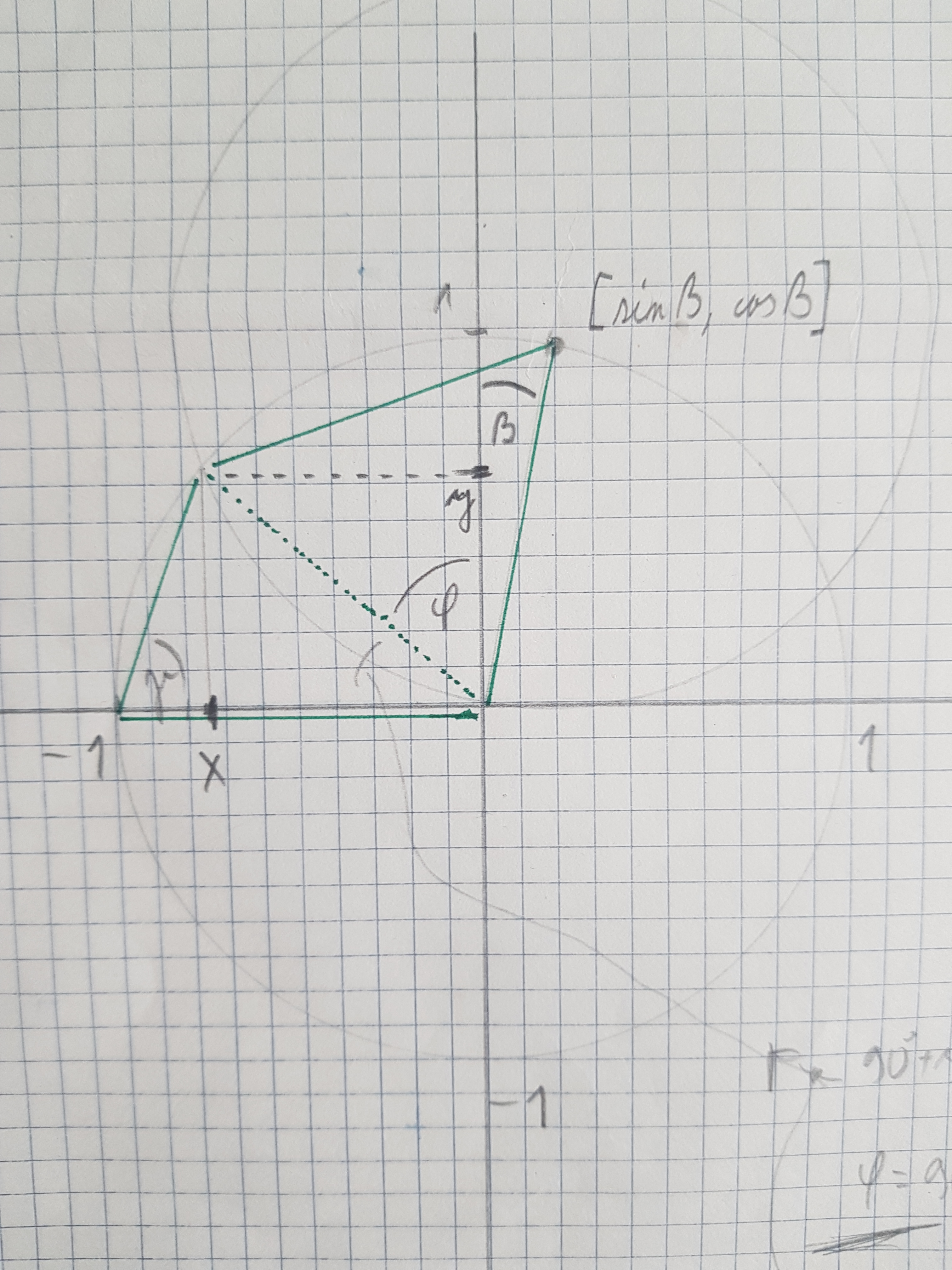
Zaviedol som ďalej vo svojom obrázku uhol \(\beta\) a uhol \(\phi\).
Keď si predstavíme, že "krútime" rovnostranný \(\triangle\) BCD okolo bodu B,
je úplne jasné, že \(\phi = 60° - \beta \).
Bod D má súradnice [x, y] a je spoločným bodom kružnice so stredom
v počiatku = bod B - s polomerom 1 a kružnice so stredom v bode
C = [\(\sin \beta, \cos \beta\)] tiež s polomerom 1.
Riešme teda sústavu rovníc
\[x^2 + y^2 = 1\]
\[(x - \sin\beta)^2 + (y - \cos\beta)^2 = 1\]


Riešenie je
\[x_{1,2} = {\sin\beta \pm \sqrt{3}\cos\beta \over 2}\]
Budem sa naďalej zaoberať len bodom vo štvrtom kvadrante,
ktorý má x-ovú súradnicu zápornú a teda
\[x = {\sin\beta - \sqrt{3}\cos\beta \over 2}\]
Opustím teraz súradnicovú sústavu a napíšem, že
\[\sin\phi = |x|\]
keďže x je záporné
\[\sin\phi = {\sqrt{3}\cos\beta - \sin\beta \over 2}\]
Nasledujúci vzorec je obecne známy
\[\sin(\alpha \pm \beta) = \sin\alpha\cos\beta \pm \cos\alpha\sin\beta\]
Ďalej vieme, že \(\sin 60° = {\sqrt 3 \over 2}\) a \(\cos 60° = {1 \over 2}\), takže
\[\sin \phi = \sin( 60° - \beta)\]
\[\sin \phi = {\sqrt{3} \over 2}\cos\beta - {1 \over 2}\sin\beta\]
\[\sin\phi = {\sqrt{3}\cos\beta - \sin\beta \over 2}\]
Hurá, dospeli sme k zhode, ale sebaironicky (citujúc klasikov)
musíme poznamenať, že to je výsledok, nad ktorým prejaví úžas
jediný človek na svete - a to naša mama.
A s uhlom \(\gamma\) to bude ešte horšie.
Dosť ľahko si overíte, že
\[\gamma = { 150° - \beta \over 2}\]
a našťastie existuje vzorec
\[\tan{\alpha \over 2} = {1 - \cos \alpha \over \sin \alpha}\]
Dáme tieto dve veci dokopy

a dostaneme
\[\tan \gamma = {2 +\sqrt{3}\cos\beta - \sin\beta \over \cos\beta + \sqrt{3}\sin\beta }\]
Vyjadrenie \(\tan\gamma\) z x a y, t.j. zo súradníc bodu D vedie k nechutnému výrazu.
Trochu lepšie to dopadne s \( \tan^2\gamma \)
\( \tan^2\gamma = {y^2 \over x^2} = {1 - x^2 \over (-1 -x)^2}
= {(1-x)(1+x) \over (1+x)^2} = {1-x \over 1+x}\)
\[\tan^2 \gamma = {2 - \sin\beta +\sqrt{3}\cos\beta \over 2 + \sin\beta - \sqrt{3}\cos\beta }\]
Tvrdíme teda, že
\[({2 +\sqrt{3}\cos\beta - \sin\beta \over \cos\beta + \sqrt{3}\sin\beta })^2
= {2 - \sin\beta +\sqrt{3}\cos\beta \over 2 + \sin\beta - \sqrt{3}\cos\beta }\]
Napodiv to je pravda:







